A Case Against Strong Longtermism

A response to Hilary Greaves and William MacAskill (part 1/4)

Unless and until some objection proves damning, we should be predisposed towards believing axiological strong longtermism.

- Hilary Greaves and William MacAskill, The Case for Strong Longtermism

The first of a four part series on longtermism and bayesian epistemology.

Preliminaries
The foundational assumptions of longtermism
What’s all the fuss with expected values anyway?
In expectation, the future is undefined
We should prefer good things to happen sooner
Conclusion
Footnotes

Preliminaries

Update 21/12/2020: Oops I was sloppy with the chronology in this paragraph - Patrick points out that the paper formalizes and extends ideas that have existed in the community for a while.

I will primarily focus on The case for strong longtermism, listed as “draft status” on both Greaves and MacAskill’s personal websites as of November 23rd, 2020. It has generated quite a lot of conversation within the effective altruism (EA) community despite its status, including multiple podcast episodes on 80000 hours podcast (one, two, three), a dedicated a multi-million dollar fund listed on the EA website, numerous blog posts, and an active forum discussion.

The profusion of philosophical jargon which permeates this paper needs to be discussed at the onset. All fields develop idiosyncratic terminology, mainly to simplify certain ideas that recur frequently within the field. However, unlike say petroleum engineering or tax accounting, we are all in the field of morality, and so it’s important to strip away the jargon terms so everyone has equal access to the underlying ideas.

This is important for another reason as well. In Politics and the English Language, Orwell warns of the dangers of political euphemism:

Defenseless villages are bombarded from the air, the inhabitants driven out into the countryside, the cattle machine-gunned, the huts set on fire with incendiary bullets: this is called pacification. Millions of peasants are robbed of their farms and sent trudging along the roads with no more than they can carry: this is called transfer of population or rectification of frontiers. People are imprisoned for years without trial, or shot in the back of the neck or sent to die of scurvy in Arctic lumber camps: this is called elimination of unreliable elements. Such phraseology is needed if one wants to name things without calling up mental pictures of them.

Consider for instance some comfortable English professor defending Russian totalitarianism. He cannot say outright, ‘I believe in killing off your opponents when you can get good results by doing so’. Probably, therefore, he will say something like this:

‘While freely conceding that the Soviet regime exhibits certain features which the humanitarian may be inclined to deplore, we must, I think, agree that a certain curtailment of the right to political opposition is an unavoidable concomitant of transitional periods, and that the rigors which the Russian people have been called upon to undergo have been amply justified in the sphere of concrete achievement.’

The inflated style itself is a kind of euphemism. A mass of Latin words falls upon the facts like soft snow, blurring the outline and covering up all the details (emphasis in original).

Euphemisms are pretty words for nasty things, and while philosophical jargon terms like “axiological”, “deontic”, “ex post”, “ex anti” and so on, aren’t exactly euphemisms, they serve the same function here, because they obscure from the reader just what exactly longtermism implies.

To reiterate, longtermism gives us permission to completely ignore the consequences of our actions over the next one thousand years, provided we don’t personally believe these actions will rise to the level of existential threats. In other words, the entirely subjective and non-falsifiable belief that one’s actions aren’t directly contributing to existential risks gives one carte blanche permission to treat others however one pleases. The suffering of our fellow humans alive today is inconsequential in the grand scheme of things. We can “simply ignore” it - even contribute to it if we wish - because it doesn’t matter. It’s negligible. A mere rounding error.

The monumental asymmetry between the present and future that the longtermists seem to be missing is that the present moves with us, while the future never arrives. Concretely, this means that longtermism encourages us to treat our fellow brothers and sisters with careless disregard for the next one thousand years, forever. There will always be the next one thousand years.

The response to this simple observation? More jargon¹. Label this the “non-aggregationalist view”, and refute it in the inflated style of Orwell’s English professor:

However, this will amount to an argument against axiological strong longtermism only if non-aggregationism is itself an axiological view. But in fact, there are serious obstacles to interpreting non-aggregationism in axiological terms: non-aggregationist views generate cycles, and there is a widespread consensus (pace Temkin (2012)) that axiology cannot exhibit cycles (Broome 2004 pp.50-63; Voorhoeve 2013). Those who are sympathetic to non-aggregationism therefore tend themselves to interpret the view in purely deontological, rather than in axiological, terms (Voorhoeve 2014). (cf. section 4.3)

I mention this at the onset in an attempt to inoculate the reader against euphemistic jargon which can be used to justify atrocities (provided, of course, that the atrocities are non-existential and take place within one thousand years). No single individual is more of an expert in morality than another, and we all have a right to ask for these ideas to be expressed in plain english.

Question: How is it possible that the soft spoken and compassionate moral philosopher and founder of the effective altruism movement can defend a philosophy which says we shouldn’t care at all how we treat one another² for the next thousand years (provided we believe our actions won’t exacerbate existential risks)?

Answer: The pernicious and stultifying effects of bayesian epistemology, which reduces all important questions to trivial expected value calculations, and when applied to moral philosophy, amounts to repeatedly multiplying powers of ten together and gaping awestruck at the results.

Bayesian epistemology³ is Orwellian political euphemism fortified mathematically. If Oxford professors are telling their readers that some mathematical identity called “expected values” can be used to peer 1 billion years into the future, who amongst their readers would feel comfortable saying otherwise? If latin words obscure facts “like soft snow, blurring the outline and covering up all the details”, then mathematical equations are like flash-bang grenades - obscuring facts by leaving the reader stunned, confused, and bewildered.

What is particularly striking is the authors seem utterly oblivious to the fact that something might be wrong with the framework itself. In Section 4 they anticipate objections to longtermism, but at no point do they question whether using expected value calculus might itself be the cause of the repugnant conclusions they arrive at. Instead, they obediently follow the calculus and endorse the conclusions.

I’m reminded of the famous This Is Water speech from David Foster Wallace in which he describes being imprisoned by a worldview, and remarks that some imprisonments are so total, so absolute, that the prisoners don’t even realize they’re locked up.

And so it’s worth holding in mind the idea that the framework itself might be the problem, when reading defenses of longtermism written by those reluctant to step outside of, or even notice, the framework in which they are imprisoned. I’ve proposed Karl Popper’s critical rationalism as an alternative framework here before and won’t dwell on it too much in this post. Instead, I’ll mainly focus on criticizing longtermism by demystifying the expected value calculus (no, it cannot peer 1 billion years into the future), and by challenging the two major assumptions upon which longtermism is premised.

The foundational assumptions of longtermism

In Section 2 the authors helpfully state the two assumptions which longtermism needs to get off the ground:

In expectation, the future is vast in size. In particular they assume the future will contain at least 1 quadrillion ($10^{15}$) beings in expectation.
We should not be biased towards the present.

I think both of these assumptions are false, and in fact:

In expectation, the future is undefined.
We should absolutely be biased towards the present.

We’ll discuss both in turn after an introduction to expected values.

What’s all the fuss with expected values anyway?

Mathematicians tend to think of expected values the way they think of the pythagorean theorem - i.e. as a mathematical identity which can be useful in some circumstances. But within the EA community, expected values are taken very seriously indeed.⁴ One reason for this is the link between expected values and decision making, namely that “under some assumptions about rational decision making, people should always pick the project with the highest expected value”. Now, if my assumptions about rational decision making lead to fanaticism, paradoxes, and cluelessness, I might revisit the assumptions. But assuming we don’t want to do that, how should we think about expected values?

Let’s start with the definition:

\[\mathbb{EU}[A] = \sum_{ i } p_i \cdot u_i\]

Okay let’s describe this equation⁵ piece by piece. The left-hand side is the “expected utility”⁶ for action $A$. It is a single number (like $53.1342$ for example), and this number will be compared to the number obtained for action $B$ (like $23.9112$). Then a “rational decision maker” is told to choose whichever action produces a larger number (action $A$ in this hypothetical example). How do we compute the expected utility? Let’s add some annotations:

At this point you should be asking “yes, okay, but where do these probabilities and utilities come from? And come to think of it, how can we possibly know all the consequences of given action?”.

Like most things, it depends. In engineering and computer science applications, for example, probabilities are carefully measured from data, utilities are chosen pragmatically in order to achieve certain goals (i.e getting a robot to walk across a room), and the consequences associated with each action can be learned over time through experience (i.e as the robot bumps into walls.)

Meanwhile, in the land of bayesian epistemology, data doesn’t need to enter the picture at all. To illustrate this, let’s revisit Shivani’s reasoning in the previous quotation. Shivani is using the expected value equation above to gain knowledge about what will happen in the future. Specifically, she’s considering whether to move her philanthropic donation of $10,000 from the Against Malaria Foundation, which will save approximately $3$ lives in expectation, to charities aimed at preventing global domination by a totalitarian world government regime, which she calculates will save $100$ lives in expectation. Her reasoning can be represented like this

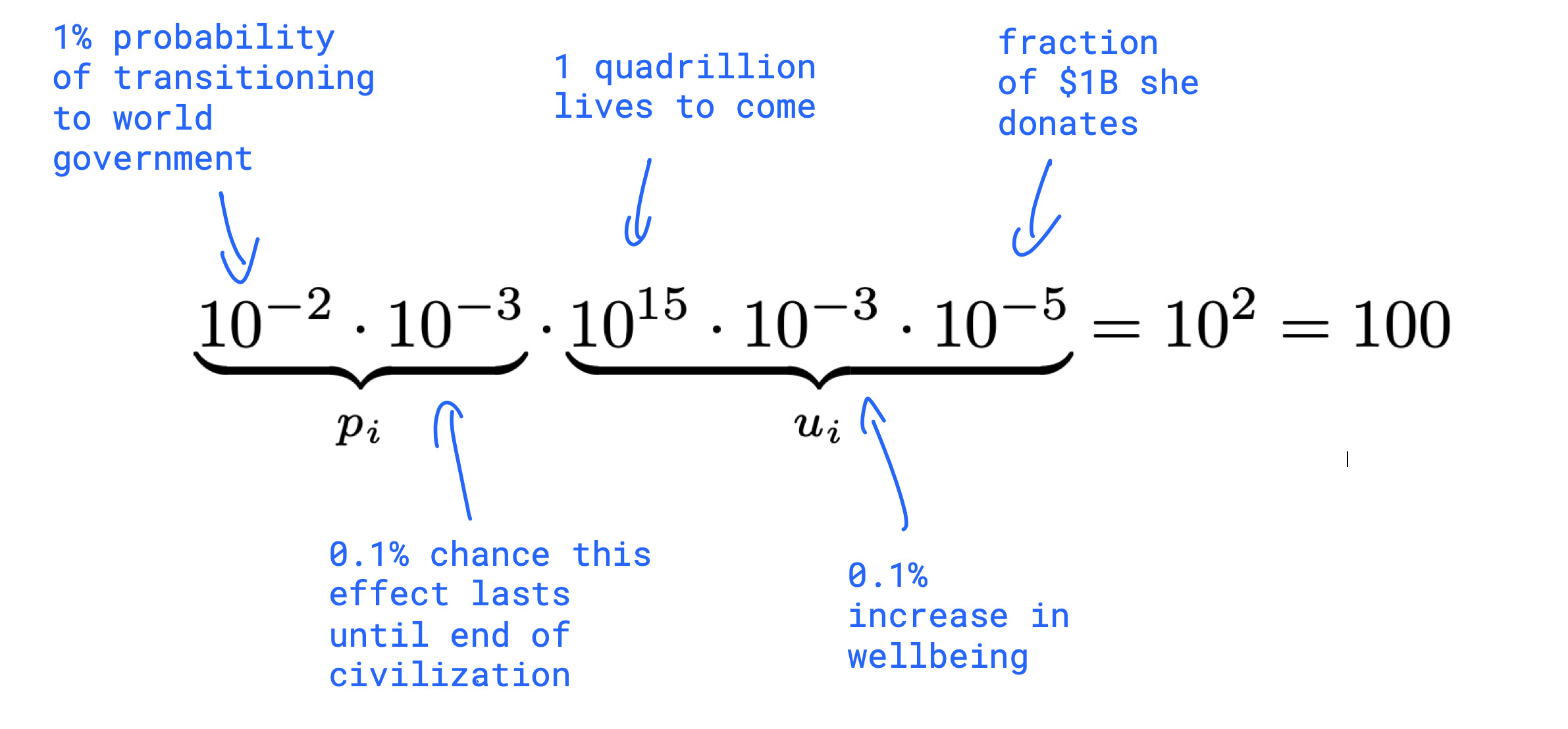
where the summation has disappeared because we’re only considering one consequence: world domination by a repressive global political regime. A similar calculation yields a whopping $100 000$ lives when considering world domination by a superintelligent AI. Clearly Shivani should move her money away from the Against Malaria Foundation, with its measly $3$ lives⁷.

But wait! We’re not comparing like with like! The expectation in the world domination by a repressive global political regime case comes from entirely made up numbers, while in the Against Malaria case come from meticulous measurements and calculations. Of all the links in this piece, I encourage the reader to click on this one in particular (which comes from Greaves and MacAskill’s footnote 22), to get a sense of the diligence and seriousness GiveWell brings to charitable donations. All this would be thrown out entirely, and replaced with arbitrary numbers pulled out of thin air, if Shivani’s reasoning is considered permissible.

The point is that all probabilities are not created equal. Even though the math is the same in both cases, the equations represent very different underlying methodologies - one has data behind it, carefully collected by measuring and learning about the world, and the other does not. The probabilities represent knowledge in one case, but only ignorance in the other.

But yet these two processes are compared by the authors as if they were equivalent. Why might they do this?

The answer I think lies in an oft-overlooked fact about expected values: that while probabilities are random variables, expectations are not. Therefore there are no uncertainties associated with predictions made in expectation. Adding the magic words “in expectation” allows longtermists to make predictions about the future confidently and with absolute certainty.

This isn’t true of course, because of an impossibility result in epistemology discussed below, but I suspect this is one of the reasons why bayesian epistemology is so enticing, and why the authors are quick to overlook the fact that all probabilities are not created equal. Because according to this framework, the expected value calculus allows you to convert uncertainty into certainty.

It allows you to say things like “Sure, we’re really uncertain about what is going to happen 1 billion years from now. But not in expectation! In expectation we know exactly what will happen in the future. And in fact, we’re so confident that we’re willing to make decisions right now based on this knowledge.” In other words, uncertainty is no longer a problem - expected values lets you get around it.

So let’s return to the questions I began with. Why all the fuss about expected values, and how should we think about them? Here are some things to keep in mind as you’re going through the literature yourself:

Expected values aren’t magic, and they cannot give you special insight into the consequences of your actions 1 billion years from now. They’re a mathematical identity which can be useful in certain circumstances - particularly when used in conjunction with data. They are not an oracle which can shape future action.
Probabilities and utilities are just numbers, and it is important to inquire about where exactly these numbers came from. Are the probabilities computed by measuring something in reality, like outcomes of coin flips or malaria rates in a particular geographic location? Or are they just assumed into existence?
Don’t take the relationship between the mathematical concept of a random variable, and the psychological/epistemological phenomenon of uncertainty, too seriously. It is a useful metaphor in some instances, but that’s about it. We can’t reduce uncertainty about the future by saying “in expectation”.

Okay, with that rather extended preamble, let’s turn to the foundational assumptions of longtermism.

In expectation, the future is undefined

The set of all possible futures is infinite, regardless of whether we consider the life of the universe to be infinite. Why is this? Add to any finite set of possible futures a future where someone spontaneously shouts “$1$”!, and a future where someone spontaneously shouts “$2$”!, and a future where someone spontaneously shouts “$3$!” …

While this may seem like a trivial example, it has crucial implications for the ways in which we talk about probabilities and expectations. Namely, reasoning about probabilities over infinite, arbitrary futures is a fundamentally meaningless exercise.

In the spirit of Hilbert’s Grand Hotel, let’s consider an infinite sequence of white and black balls in alternating order⁸

\[W~B~W~B~W~B~W~B~W...\]

Our intuitions might tempt us to say that the proportion or “relative frequency” of white balls and black balls in this infinite sequence is $1:1$, which would lead to the “probability” of drawing a black ball being $\textbf{1}/\textbf{2}$.

However, let’s now imagine reordering the infinite set as follows:

\[B~B~W~B~B~W~B~B~W~B~B~W...\]

From the perspective of longtermism, these black balls might represent possible futures in which we’ve been annihilated by a given existential risk. But what do we think the “probability” of observing a black ball is now? It appears to be $2/3$! We could imagine doing this again and again, so that the “probability” moves from $2/3$, to $4/5$, to $5/6$, ad infinitum.

Clearly, there is a problem here. For this reason, “the probability of drawing a black ball” from this infinite set literally has no meaning. It’s undefined. We are used to estimating probabilities by tallying up counts, and dividing by a denominator. This clearly works over finite sets, where the denominator is just the count of all total observations⁹, but in infinite sets this results in $\infty / \infty$, which again, is undefined.

This is known as a “veridical paradox” - a result that appears absurd, but is demonstrated to be true nonetheless. Wikipedia describes the situation succinctly:

Initially, this state of affairs might seem to be counter-intuitive. The properties of “infinite collections of things” are quite different from those of “finite collections of things”. The paradox of Hilbert’s Grand Hotel can be understood by using Cantor’s theory of transfinite numbers. Thus, while in an ordinary (finite) hotel with more than one room, the number of odd-numbered rooms is obviously smaller than the total number of rooms. However, in Hilbert’s aptly named Grand Hotel, the quantity of odd-numbered rooms is not smaller than the total “number” of rooms. (emphasis mine)

But don’t we apply probabilities to infinite sets all the time? Yes - to measurable sets. A measure provides a unique method of relating proportions of infinite sets to parts of itself, and this non-arbitrariness is what gives meaning to the notion of probability. While the interval between 0 and 1 has infinitely many real numbers, we know how these relate to each other, and to the real numbers between 1 and 2.

By contrast, we do not have a measure over the set of white and black balls, or over the set of infinite futures. In the above example, we saw that this allowed us to shuffle the ordering so as to rig the deck in favor of whichever outcome we wanted. For this reason, probabilities, and thus expectations, are undefined over the set of all possible futures.

This observation - that in expectation, the future is not vast, but undefined - passes a few basic sanity checks. First, we know from common sense that we cannot predict the future, in expectation or otherwise. Prophets have been trying this for millennia with little success - it would be rather surprising if the probability calculus somehow enabled it.

Second, we know from basic results in epistemology (discussed here before) that predicting the future course of human history is impossible when that history depends on future knowledge, which we by definition don’t know. We cannot know today what we will only learn tomorrow. It is not the case that someone standing in 1200 would assign a “low credence” to the statement “the internet will be invented in the 1990’s”. They wouldn’t be able to think the thought in the first place, much less formalize it mathematically.

We should prefer good things to happen sooner

In Section 2.2 they state their second assumption:

Our second assumption is that, for the purposes of moral decision-making and evaluation, all the consequences of one’s actions matter, and (once we control for the degree to which the consequence in question is predictable at the time of action) they all matter equally.

In particular, this assumption rules out a positive rate of pure time preference. Such a positive rate would mean that we should intrinsically prefer a good thing to come at an earlier time rather than a later time. If we endorsed this idea, our argument would not get off the ground.

To see this, suppose that future well-being is discounted at a modest but significant positive rate — say, 1% per annum. Consider a simplified model in which the future certainly contains some constant number of people throughout the whole of an infinitely long future, and assume for simplicity that lifetime well-being is simply the time-integral of momentary well-being. Suppose further that average momentary well-being (averaged, that is, across people at a time) is constant in time. Then, with a well-being discount rate of 1% per annum, the amount of discounted well-being even in the whole of the infinite future from 100 years onwards is only about one third of the amount of discounted well-being in the next 100 years. While this calculation concerns total well-being rather than differences one could make to well-being, similar considerations will apply to the latter.

Having a “positive rate of pure time preference” simply means that one is biased towards the present - that is, one discounts future well-being. Graphically, the difference between discounted and undiscounted future well-being can be represented as follows:

Figure 1: The "all consequences matter equally" assumption.

If one does not discount the future, then one is equally concerned about every moment in time, hence the phrase “all consequences matter equally”. Mathematically, this implies (with the unbounded future assumption) that there is an infinite amount of possible well-being in the future to concern ourselves with (the pink area above). This assumption is why longtermism states it is always better to work on x-risks than anything else one might want to do to improve the short-term.

That is, that pink well of utility ($u_i$ above) will always be large enough to compensate for any arbitrarily small probability ($p_i$) of a successful intervention.

This last point can be understood like this:

Figure 2: The utility of different actions according to longtermism (cf. section 2.3).

Thus with these assumptions, they have unintentionally granted themselves unlimited flexibility to adjust $u_i$ and $p_i$ so that the pink line always overtakes the grey one. This puts the “strong” into “strong longtermism” and is what they say “renders axiological strong longtermism plausible”.

I think however, that it just renders strong longtermism unfalsifiable. Nothing could possibly refute an argument like this, because there are an unlimited number of degrees of freedom to adjust, and no data to be constrained by¹⁰. These degrees of freedom can always be tuned to strip funding for any charitable organization whatsoever. It could even be used to squash funding for “x-risks” themselves, by inventing an even larger class of risk (“super x-risks”), with even larger utilities and probabilities, and playing their argument back at them. This is frivolous.

Still, we must address the content of their assumption in order to decide if it’s reasonable. We can simplify their second paragraph to see more plainly the position they endorse:

We should not be biased towards the present.

It appears to me that such an extreme position must be argued for, and not simply asserted. But disappointingly, the only argument they provide is:

For present purposes, we take the assumption of a zero rate of pure time preference to be fairly uncontroversial. We know of no moral philosophers and few theoretical economists who defend a non-zero rate of pure time preference.

I’m tempted to invoke Hitchens’s razor here, that “What can be asserted without evidence can be dismissed without evidence”. But that feels like a bit of a cop-out, so I’ll attempt to make the opposite case, namely:

One should absolutely be biased towards the present.

This seems to follow almost immediately from another assumption made by the authors - that there might be an impending x-risk in the future. We should be biased towards the present for the simple reason that tomorrow may not arrive. The further out into the future we go, the less certain things become, and the smaller the chance is that we’ll actually make it there. Preferring good things to happen sooner rather than later follows directly from the finitude of life.

And let us not forget that good things don’t happen to us, they happen because of us. We are not just waiting arms outstretched for “good things” to be sprinkled down to us from the heavens. We are (all of us, humanity as a whole) the ones actively working to bring these good things about. I cannot improve¹¹ upon Popper’s words when he says:

Work for the elimination of concrete evils rather than for the realization of abstract goods. Do not aim at establishing happiness by political means. Rather aim at the elimination of concrete miseries. Or, in more practical terms: fight for the elimination of poverty by direct means–for example, by making sure that everybody has a minimum income. Or fight against epidemics and disease by erecting hospitals and schools of medicine. Fight illiteracy as you fight criminality. But do all this by direct means. Choose what you consider the most urgent evil of the society in which you live, and try patiently to convince people that we can get rid of it.

But do not try to realize these aims indirectly by designing and working for a distant ideal of a society which is wholly good. However deeply you may feel indebted to its inspiring vision, do not think that you are obliged to work for its realization, or that it is your mission to open the eyes of others to its beauty. Do not allow your dreams of a beautiful world to lure you away from the claims of men who suffer here and now. Our fellow men have a claim to our help; no generation must be sacrificed for the sake of future generations, for the sake of an ideal of happiness that may never be realized. In brief, it is my thesis that human misery is the most urgent problem of a rational public policy and that happiness is not such a problem. The attainment of happiness should be left to our private endeavours.

It is a fact, and not a very strange fact, that it is not so very difficult to reach agreement by discussion on what are the most intolerable evils of our society, and on what are the most urgent social reforms. Such an agreement can be reached much more easily than an agreement concerning some ideal form of social life. For the evils are with us here and now. They can be experienced, and are being experienced every day, by many people who have been and are being made miserable by poverty, unemployment, national oppression, war and disease. Those of us who do not suffer from these miseries meet every day others who can describe them to us. This is what makes the evils concrete. This is why we can get somewhere in arguing about them; why we can profit here from the attitude of reasonableness. We can learn by listening to concrete claims, by patiently trying to assess them as impartially as we can, and by considering ways of meeting them without creating worse evils.

– Karl Popper, Conjectures and Refutations, Utopia and Violence (emphasis mine.)

This is the reason why we should be biased towards right now - because right now is the only time we have to help those who are suffering. It will always be now. We should prefer good things to happen sooner, because that might help us to bring these good things about.

In short, there is a lot of work still to be done. We needn’t play games with probability, or spend time developing sophisticated philosophical terminology that allows one to ignore data. All that is needed to make moral progress is to recognize that present day suffering exists right now in abundance, and that together we can work to understand it and alleviate it.

Conclusion

I believe that by combining the heart and the head — by applying data and reason to altruistic acts — we can turn our good intentions into astonishingly good outcomes. (…)

Effective altruism is about asking, “How can I make the biggest difference I can?” and using evidence and careful reasoning to try to find an answer. It takes a scientific approach to doing good. Just as science consists of the honest and impartial attempt to work out what’s true, and a commitment to believe the truth whatever that turns out to be, effective altruism consists of the honest and impartial attempt to work out what’s best for the world, and a commitment to do what’s best, whatever that turns out to be.

-William MacAskill, Doing Good Better: How Effective Altruism Can Help You Make a Difference.

So what might an alternative to longtermism look like? Simply returning to the excellent advice given by MacAskill in his first book. Somewhere along the way, in his noble efforts to make altruism more effective, he has forgotten about the data and evidence components of the scientific approach. MacAskill and Greaves say the argument they are making is “ultimately a quantitative one.” But what does it mean to apply the quantitative method in the absence of data? What exactly are they applying the quantitative method to?

Near the end of Conjectures and Refutations, Popper criticizes the Utopianist attitude of those who claim to be able to see far into future, who claim to see distant far away evils and ideals, and who claim to have knowledge that can only ever come from “our dreams and from the dreams of our poets and prophets”. Against this Popper replies:

The Utopianist attitude, therefore, is opposed to the attitude of reasonableness. Utopianism, even though it may often appear in a rationalist disguise, cannot be more than a pseudo-rationalism.

… if among our aims and ends there is anything conceived in terms of human happiness and misery, then we are bound to judge our actions in terms not only of possible contributions to the happiness of man in a distant future, but also of their more immediate effects. We must not argue that the misery of one generation may be considered as a mere means to the end of securing the lasting happiness of some later generation or generations; and this argument is improved neither by a high degree of promised happiness nor by a large number of generations profiting by it. All generations are transient. All have an equal right to be considered, but our immediate duties are undoubtedly to the present generation and to the next. Besides, we should never attempt to balance anybody’s misery against somebody else’s happiness.

– Conjectures and Refutations, Utopia and Violence (emphasis mine.)

and with this, “the apparently rational arguments of Utopianism dissolve into nothing.”

Huge thanks to Ben Chugg and Rob Brekelmans for the multiple rounds of detailed feedback, as well as Halina, David, Chesto, Dania, and Izzy for their many helpful suggestions

Footnotes

A friend asked me to clarify what I meant here. By “this observation” I just mean the fact that longtermism is a really really bad idea because it lets you justify present day suffering forever, by always comparing it to an infinite amount of potential future good (forever). This concern they summarize by saying:

… many ethical theorists are sympathetic to a non-aggregationist view, according to which, when large benefits or harms to some are at stake, sufficiently trivial benefits or harms to others count for nothing at all from a moral point of view. (Scanlon 1998:235, Frick 2015, Voorhoeve 2014.) In the above example, such a view would indeed tend to hold that one ought to save a life rather than deliver even an arbitrarily large number of lollipop licks (emphasis in original).

So here is how I parse this sentence. First I’ll make the following substitutions, which I think are justified given that this concern is raised by the authors as an objection to longtermism:
- “one ought to save a life” -> “one ought to work to eliminate present day suffering”
- “deliver even an arbitrarily large number of lollipop licks” -> “work to produce an infinite amount of potential future happiness” (spread however thinly between individuals)
Then the non-aggregationist position “indeed tends to hold” that one ought to work to eliminate present day suffering rather than work to produce an infinite amount of potential future happiness (which they are against). This they claim to refute in the quote above, which I’m not even going to attempt to parse. I maintain my claim that they use jargon to dodge the question. ↩
I should say here that of course MacAskill and Greaves don’t want any harm to befall any of their fellow humans, and MacAskill in particular has done more for the betterment of humanity than most other public figures I can name. I trust that nothing said here will be taken as an attack on their character, and only this one particular idea. ↩
By “Bayesian Epistemology” I mean what David Deutsch describes here. ↩
I invite the reader to google for instance “expected values effective altruism” or “expected values less wrong” to see what I mean. ↩
If there is a continuous range of things that can happen (for example, changing the angle of a robot arm), then the summation is replaced with an integral and the equation looks a little more complicated, but the concept remains the same. ↩
The concept of “expected values” and “expected utilities” are interchangeable for our purposes, but one can think of expected utilities as expected value theory applied to utilities. ↩
Note that Shivani would not have had to move her money had the authors assumed a mere ten trillion people into existence. ↩
I am modifying slightly an argument from David Deutsch in Chapter 8 of The Beginning of Infinity. ↩
Using Jaynes’ axiomatization is no use here either - he has a strict finite sets policy in place, and explicitly warns of the “careless use of infinite sets” (cf. Section 2.5 and Chapter 15 “Paradoxes of probability theory” in The Logic of Science). ↩
See for instance sections 2.1, 2.2, 2.3, 3.1, 3.3, and the last few paragraphs of 3.4. Each set of assumptions corresponds to another line in Figure 2. ↩
Apologies for the length, I couldn’t help but quote in full. ↩